AAPG '98 Annual Convention, Advances in Geostatistics, Salt Lake City, Utah, May 17-20, 1998.
William L. Wingle and
Eileen P. Poeter,
Colorado School of Mines,
Department of Geology and Geological Engineering
It is often difficult to fit a model semivariogram to both the principle-axis and the minor-axes using traditional methods with anisotropy ratios. Traditionally, models (possibly nested) are modified with anisotropy factors; these represent the relative range of the semivariogram for three orthogonal axes. This technique is restrictive, and this discussion presents a method for relieving this limitation by defining different semivariogram models, independently for each axis. These are referred to as directional semivariograms. The process increases the kriging processing time by 80% to 200%, but the method offers the modeler greater flexibility, and simulation or estimation results that are more representative of the site, because the spatial variation of the data can be more precisely defined.
Introduction
Semivariogram modeling is the foundation for geostatistical analysis, and can also be the most difficult and time consuming portion of the analysis. In part, this is due to the computationally intensive calculations, but it is also due to the difficulty in defining semivariogram models which reasonably honor the experimental semivariograms in the principle and minor search directions. With current techniques that use anisotropy factors (Englund and Sparks, 1988; Journel and Huijbregts, 1978; Deutsch and Journel, 1992), often it is not possible to model all the orthogonal experimental semivariograms exactly. Consequently compromises are required for the definition of one, or even all of the models. If the compromises are not too substantial, then this approach is acceptable, because, generally the kriged results are relatively insensitive to minor changes in the semivariogram. Although this insensitivity offers some comfort, a method that economizes human time and offers more precision is preferable. This paper describes a procedure, which allows the modeler to define a unique semivariogram model for each orthogonal axis of the experimental semivariogram.
Theory
This algorithm uses components of each model to determine ![]() (h) values between the axes.
Anisotropy factors are not used, rather the modeler specifies the number of nests,
sills, ranges, and model structure types independently for each axis. The only
requirements are 1) the nugget must be the same for all models, and 2) the total sill
must be the same at infinity. These two requirements are not particularly restrictive.
Requiring the nugget to be the same is reasonable, because at zero distance, direction
is irrelevant. The requirement that the total sill components are equal ensures that
the kriging matrix is not singular. If different sills are desired, then this
requirement is met by defining an extremely large range for the final nest to make up
the balance of the sill component. The error introduced by the final nest has no
significant affect on the area of interest.
(h) values between the axes.
Anisotropy factors are not used, rather the modeler specifies the number of nests,
sills, ranges, and model structure types independently for each axis. The only
requirements are 1) the nugget must be the same for all models, and 2) the total sill
must be the same at infinity. These two requirements are not particularly restrictive.
Requiring the nugget to be the same is reasonable, because at zero distance, direction
is irrelevant. The requirement that the total sill components are equal ensures that
the kriging matrix is not singular. If different sills are desired, then this
requirement is met by defining an extremely large range for the final nest to make up
the balance of the sill component. The error introduced by the final nest has no
significant affect on the area of interest.
This technique allows the modeler to honor the results of the experimental semivariogram
analysis, thus it is easier to model the data set and the results are more accurate.
However, the calculation of ![]() (h) is substantially more complex than traditional methods,
therefore the method requires computational effort. The additional effort is comparable
to the computational effort required for the search procedure and matrix solution portions
of the kriging algorithm so, the task, only increased total processing time by about 80%
to 200% (based on observed differences in computation time for example data sets). This
is acceptable, because the semivariogram model preparation is simplified, and the
simulations or estimates more closely honor the spatial statistics of the site.
(h) is substantially more complex than traditional methods,
therefore the method requires computational effort. The additional effort is comparable
to the computational effort required for the search procedure and matrix solution portions
of the kriging algorithm so, the task, only increased total processing time by about 80%
to 200% (based on observed differences in computation time for example data sets). This
is acceptable, because the semivariogram model preparation is simplified, and the
simulations or estimates more closely honor the spatial statistics of the site.
Two steps of the kriging process are modified to incorporate directional semivariograms
into the kriging algorithm: 1) the search for nearest neighbors, and 2) the calculation
of the covariance components of the kriging matrix. The first step in estimating the
value for a grid location is to find the influential neighboring points. For isotropic
situations the nearest sample points are the best estimators. For anisotropic situations,
the best estimators are those points with the smallest spatial variance calculated
from the model semivariogram (![]() (h)). Using anisotropy factors, the sample point
locations are transformed to equivalent isotropic space, using a simple transformation
and rotation, based on the orientation of the principle model axis, and the anisotropy
factors of the minor-axes. Once transformed, the estimation variance is solely a
function of the distance between the grid location and the sample point, therefore
(h)). Using anisotropy factors, the sample point
locations are transformed to equivalent isotropic space, using a simple transformation
and rotation, based on the orientation of the principle model axis, and the anisotropy
factors of the minor-axes. Once transformed, the estimation variance is solely a
function of the distance between the grid location and the sample point, therefore
![]() (h) doesn't have to be calculated. Conventional techniques (Deutsch and Journel,
1992; Gómez-Hernández and Srivastava, 1990), use Pythagoras' Theorem to
find the closest points. When directional semivariogram models are used, direction
as well as distance is important. Consequently, a simple transformation and rotation
is not possible (Figure 1). For this reason,
(h) doesn't have to be calculated. Conventional techniques (Deutsch and Journel,
1992; Gómez-Hernández and Srivastava, 1990), use Pythagoras' Theorem to
find the closest points. When directional semivariogram models are used, direction
as well as distance is important. Consequently, a simple transformation and rotation
is not possible (Figure 1). For this reason, ![]() (h) must be calculated for each sample
in the search neighborhood, and those points with the smallest
(h) must be calculated for each sample
in the search neighborhood, and those points with the smallest ![]() (h) values are the
most influential, and thus constitute the most influential neighbors.
(h) values are the
most influential, and thus constitute the most influential neighbors.
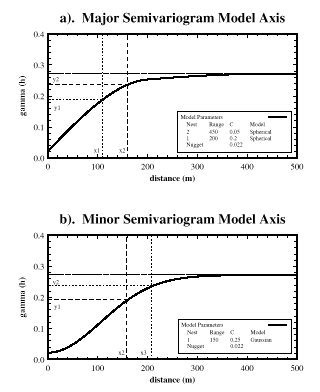
Once the most influential neighboring data points have been selected, the kriging
matrix is solved as usual, with the exception of the ![]() (h) calculation. Again, for
directional semivariograms, it is not possible to transform points into isotropic space,
therefore components of the individual axes must be resolved. Whether
(h) calculation. Again, for
directional semivariograms, it is not possible to transform points into isotropic space,
therefore components of the individual axes must be resolved. Whether ![]() (h) is calculated
to determine the most influential neighbors or individual components of the kriging matrix,
the same technique is used as described in the following section.
(h) is calculated
to determine the most influential neighbors or individual components of the kriging matrix,
the same technique is used as described in the following section.
Equations and Proof
Calculating ![]() (h) to determine the nearest neighbors for a grid location, or to define
individual components of the kriging matrix, requires the equation for an ellipsoid:
(h) to determine the nearest neighbors for a grid location, or to define
individual components of the kriging matrix, requires the equation for an ellipsoid:
![]() (1)
(1)
| Model Type | Practical Range |
|---|---|
| Spherical | range |
| Exponential | 3 x range |
| Gaussian | sqrt(3) x range |
| Linear | range |

If the unadjusted range and not the practical range is used, the axis defined with
the model using the longest practical range will be under-weighted. The equations
for determining each component ![]() (h)X,Y,Z and the resultant
(h)X,Y,Z and the resultant ![]() (h) are derived below.
The components of each axis for each structure of the nested semivariogram model can be
related through the aspect factors:
(h) are derived below.
The components of each axis for each structure of the nested semivariogram model can be
related through the aspect factors:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
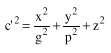 (7)
(7)
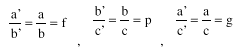 (8a, b, c)
(8a, b, c)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13a, b)
(13a, b)
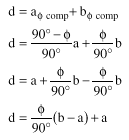 (14)
(14)
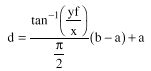 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
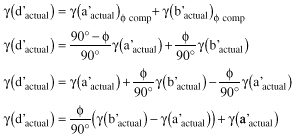 (19)
(19)
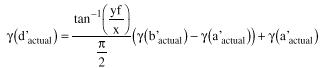 (20)
(20)
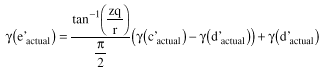 (21)
(21)
![]() (22)
(22)
The previous equations describe how the orthogonal axes can be independently defined and modeled. A possible problem with this method is it that a number of equations are merged into hybrid equations. In nested structures, this is acceptable, but Myers and Journel (1990) suggest that this may lead to non-invertible covariance matrices (i.e. models that are not positive definite) when the model equations are applied orthogonally. Positive definite matrices are required by the kriging algorithm.
Although we have not proved these hybrid equations yield positive definite matrices, the basic two- and three-dimensional problems described by Myers and Journel, do not occur. Also, several basic tests to validate the assumption of positive definiteness, are not violated (Isaaks and Srivastava, 1989):
Conclusions
This paper describes the calculation method for directional semivariograms. The procedure simplifies modeling the experimental semivariograms, because one need not compromise when selecting model types and sills for each axis. There is an increase in computational effort which increases total processing time (observed times increased 80% to 200%), but this cost is relatively minor when compared to the total time the modeler spends developing semivariogram models. Overall, use of directional semivariogram modeling requires additional computational time, but modeler effort is reduced, and a significant increase in accuracy may be attained.
Acknowledgments
We appreciate the United States Army Corps of Engineers, Waterways Experiment Station for support of this research.
References
Deutsch, C.V. and A.G. Journel, 1992, GSLIB: Geostatistical Software Library and User's Guide. New York, Oxford Press.
Englund, E. and A. Sparks, 1988, GEO-EAS. U.S. Environmental Protection Agency, Environmental Monitoring Systems Laboratory, EPA/600/4-88/033.
Gómez-Hernández, J.J. and R.M. Srivastava, 1990, ``ISIM3D: An ANSI-C Three Dimensional Multiple Indicator Conditional Simulation Program.'' Computers in Geoscience, Vol. 16, No. 4, pp. 395-440.
Isaaks, E.H. and R.M. Srivastava, 1989, An Introduction to Applied Geostatistics. New York, Oxford University Press.
Journel, A.G. and C.J. Huijbregts, 1978, Mining Geostatistics. London, Academic Press.
Myers, D.E, and A. Journel, 1990, Variograms with Zonal Anisotropies and Noninvertable Kriging Systems, Mathematical Geology, Vol. 22, No. 7, pp 779-785.